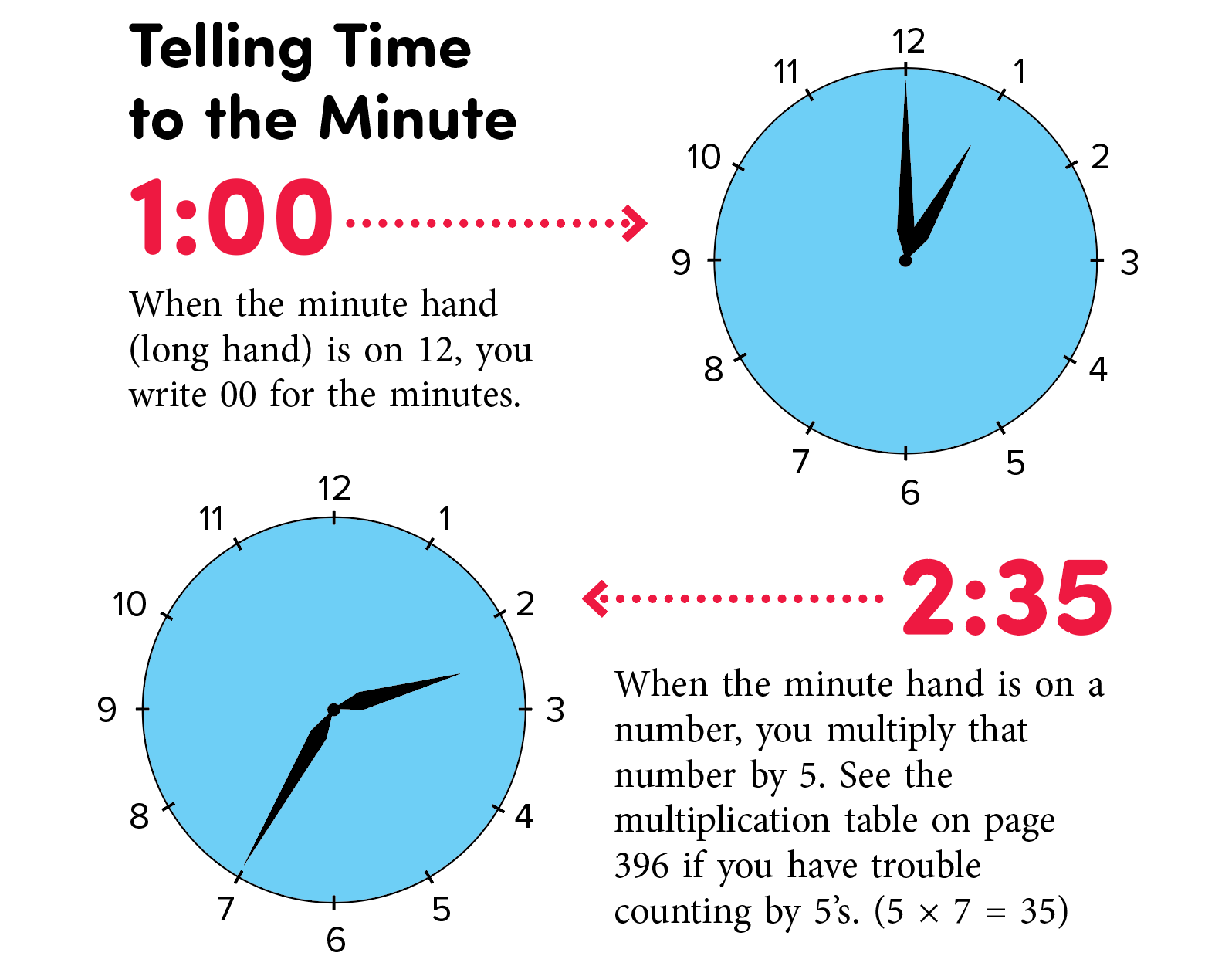
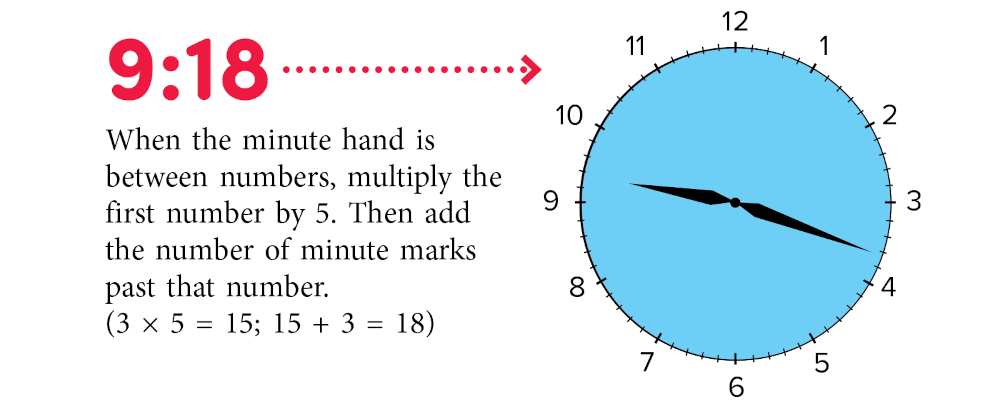
WT 390
Page 390
Improving Math Skills
When you think of math, what do you think of? Adding numbers? Counting change? Measuring with a ruler? Dividing something into equal parts?
Math is this and much more. Learning math is almost like learning a new language. Math has its own special words and symbols. Math also has its own skills and strategies. This chapter will help you understand the language and strategies of mathematics. At the end of the chapter, you will find all kinds of helpful charts and tables.

WT 391
Page 391
Solving Basic Word Problems
Most of your math assignments include at least two or three word problems. The best way to solve word problems is to follow a process. That way you won’t miss any important details. Here’s a process to try:
Four-Step Process
1. Read the problem.
Be sure you understand all the parts. Look for any key words like “how many” or “in all.”
2. Decide what you need to do.
Do you have to add a series of numbers? Do you have to multiply or subtract? Do you have to do more than one thing—maybe add, then subtract?
3. Solve the problem.
There may be more than one way to solve a problem. Page 393 shows you five strategies for figuring out the same problem. (Remember, show all of your work so you can check it later.)
4. Check your answer.
Here are two ways to check: (1) You can do the problem again, only in a different way. (2) You can start with your answer and work backward. Let’s say that your answer to a problem is 42. You multiplied 6 times 7 to get that answer. If you divide 42 by 6, you should get 7. Or if you divide 42 by 7, you should get 6.
WT 392
Page 392
Sample Word Problem
1. Read the problem.
Susan and her best friend, Maria, are making chocolate cookies for their soccer picnic. There will be 13 people at the picnic, including four parents. Susan and Maria want to give each person three cookies. How many cookies do they need to make?
2. Decide what you need to do.
After reading the problem, you know that you are looking for a total number of cookies. You also know the basic numbers you have to work with: 13 people with 3 cookies each.
3. Solve the problem.
Let’s say you decide to skip-count by three, 13 times. (See the next page for other strategies.)
3, 6, 9, 12, 15, 18, 21, 24, 27, 30, 33, 36, 39
4. Check your answer.
To check your work, you decide to solve the problem in a different way. You make tally marks in 13 groups of three (/// /// /// . . . ). You then add up all of your marks. (Your work checks out. The girls need to make 39 cookies.)
WT 393
Page 393
Five Problem-Solving Strategies
There are many different ways to solve a word problem. Five different strategies are given below. (The numbers are from the sample word problem on page 392.)
Skip-count by three, 13 times.
3, 6, 9, 12, 15, 18, 21, 24, 27, 30, 33, 36, 39
Make tally marks. Put three marks in a group, make 13 groups, and add up all the marks.
/// /// /// /// /// /// /// /// /// /// /// /// ///
Estimate and check.
Estimate: 36 cookies
Check: Divide 36 by 3 (3 ÷ 36). The answer is 12. That’s close! Three more cookies are needed, because there are 13 people, not 12. (36 + 3 = 39)
Use cubes or other counters. Make 13 groups of 3 counters. Then count them all.
Write a math problem. Multiply the number of people by the number of cookies each person would get.
13 people
× 3 cookies (each)
39 cookies (total)

WT 394
Page 394
Solving Brain Stretchers
Sometimes you are asked to do problems that can’t be solved by simply multiplying or dividing the numbers. We call these types of problems brain stretchers. Your teacher may give you these problems to get you thinking. Here’s such a problem:
You shut your eyes and reach into a jar filled with pennies, nickels, and dimes. You pull out three coins. How much money might be in your hand?
Problem-Solving Strategy
Let’s see how one person works on this problem.
✔ Write equations.
Leo starts by listing different coin combinations. (Each combination can be called an equation.)
Pennies: 1¢ + 1¢ + 1¢ = 3¢
Nickels: 5¢ + 5¢ + 5¢ = 15¢
Pennies and Nickels:
1¢ + 1¢ + 5¢ = 7¢
1¢ + 5¢ + 5¢ = 11¢
1¢ + 5¢ + 5¢ = 11¢
✔ Organize a list or table. After Leo has all the penny and nickel combinations, he lists the totals from the smallest number to the largest: 3, 7, 11, 15.
✔ Look for a pattern. Leo notices that each number is four numbers higher than the last.
✔ Complete the problem. Then Leo tries the combinations with dimes. There are six. You could try them, too. Does the pattern continue?
WT 395
Page 395
Symbols, Numbers, and Tables
Use the following symbols, tables, and charts whenever you need help with your math.
Addition and Subtraction Table
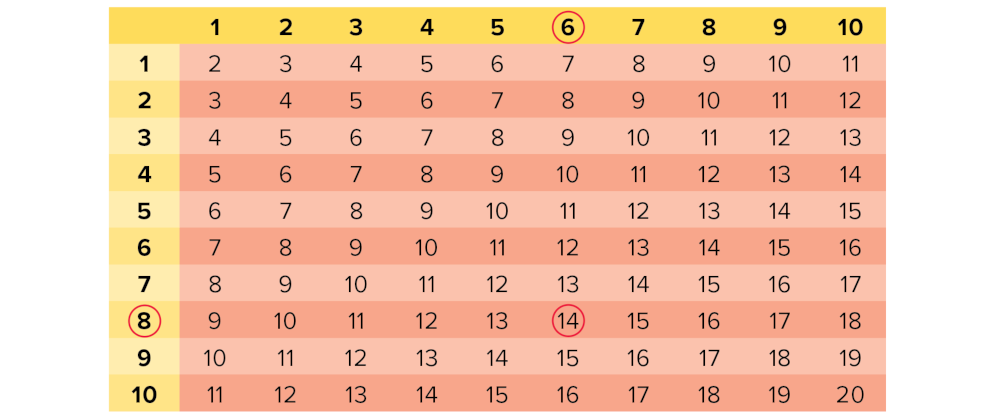
To add two numbers (8 + 6), find one of the numbers at the beginning of a row (8). Find your second number at the top of a column (6). Find your answer where the row and column meet (8 + 6 = 14).
To subtract two numbers (14 – 6), locate the larger number in the table (14). Then subtract the number at the top of the column (6). Your answer will be in the row to the far left (8).
WT 396
Page 396
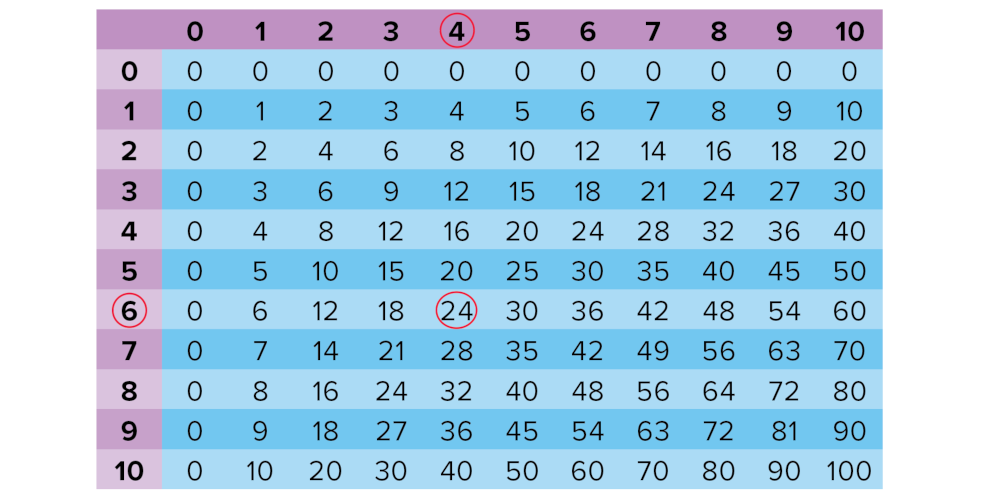
Multiplication and Division Table
To multiply two numbers (4 × 6), find one of the numbers at the top of a column (4). Find the second number at the beginning of a row (6). Find your answer where the row and column meet (6 × 4 = 24). To divide (24 ÷ 6), find the larger number in the table (24). Then divide by the number at the far left (6). Your answer is at the top of the column (4).
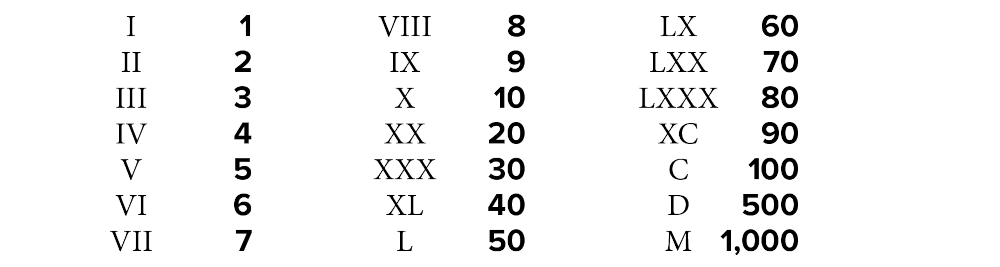
Roman Numerals
WT 397
Page 397
Rounding Numbers
You can round a number to the nearest ten, hundred, thousand, or even million.
Rounding to the Nearest Ten
If your number is 32, 32 is closer to 30 than to 40. So, 32 rounded to the nearest ten is 30.

The number 36 is closer to 40 than to 30. So, 36 rounded to the nearest ten is 40.

Numbers ending in 1, 2, 3, or 4 are rounded down. Those ending in 6, 7, 8, or 9 are rounded up. And even though 5 is right in the middle, it is rounded up. So, 35 rounded to the nearest ten is 40.

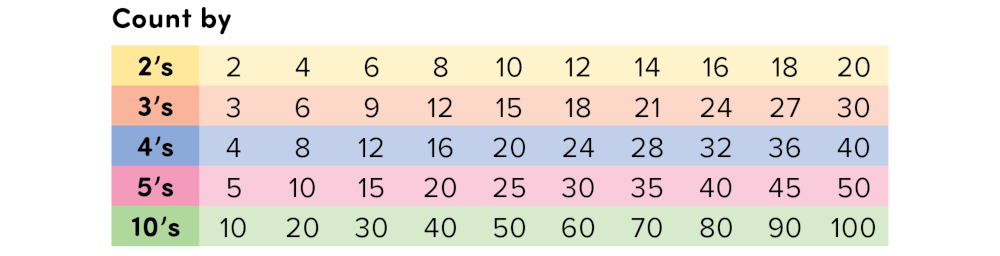
Skip-Counting
 © Thoughtful Learning 2025
© Thoughtful Learning 2025

WT 398
Page 398
Place-Value Chart

Fractions

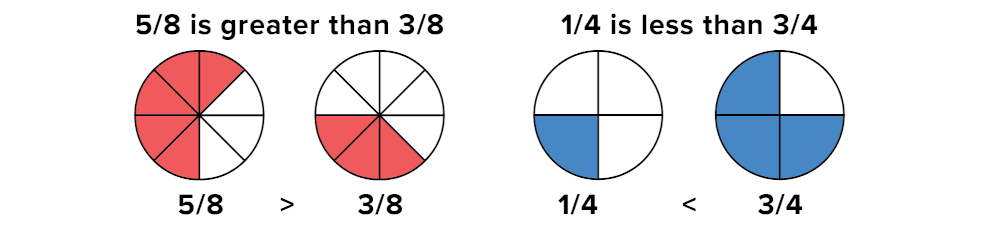
In 1/2, 1 is the numerator and 2 is the denominator. All the fractions above are called equivalent fractions. They all name the same part, or fraction, of the square . . . even though they have different numerators and denominators. Fractions with the same denominators are easy to compare.
WT 399
Page 399